हम एक उन्नत त्रिभुज गणक (Triangle Calculator) के बारे में बात करेंगे, जैसे की त्रिभुज क्या है, त्रिभुज और त्रिभुज गणक का महत्व, इस त्रिभुज गणक की विशेषताएं, और इसका उपयोग कैसे करें। साथ ही, हम त्रिभुज के 5 उदाहरणों को भी देखेंगे, जिन्हें बेहतरीन तरीके से समझाया गया है। यह कैलकुलेटर विद्यार्थियों के लिए बहुत ही महत्वपूर्ण है। यह कैलकुलेटर उनके गणतीय कैलकुलेशन को आसान बनाने में मदद करेगा।

त्रिभुज क्या है? (What is a Triangle?)

त्रिभुज एक बुनियादी ज्यामितीय आकार है। यह तीन सीधी रेखाओं (भुजाओं) से बनी एक बंद आकृति होती है, जिसमें तीन कोण होते हैं। त्रिभुज के तीनों कोणों का योग हमेशा 180 अंश होता है। त्रिभुज को भुजाओं और कोणों के आधार पर वर्गीकृत किया जा सकता है।

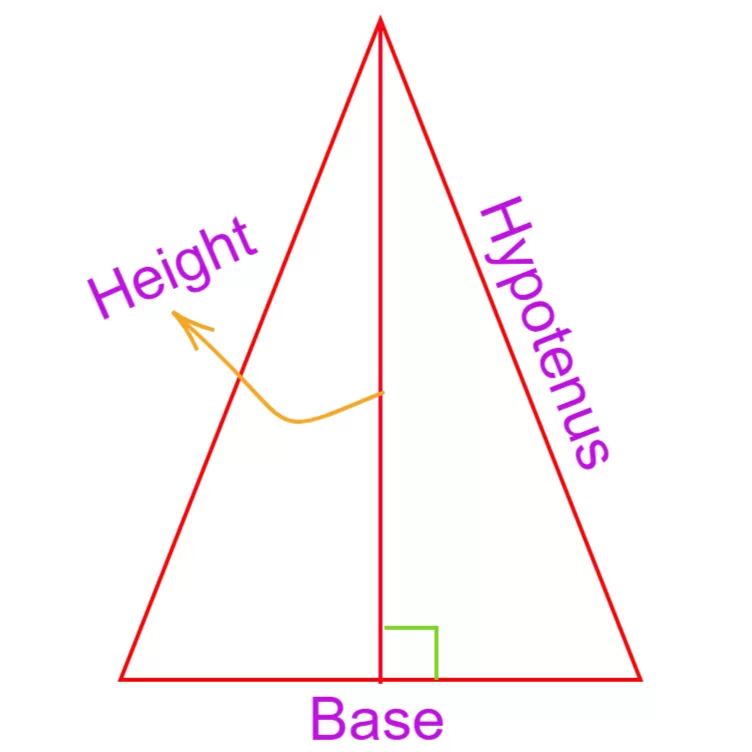
त्रिभुजों का वर्गीकरण (Classification of Triangles):

• भुजाओं के आधार पर (Based on Sides):
  • समबाहु त्रिभुज (Equilateral Triangle): तीनों भुजाएं बराबर होती हैं और तीनों कोण 60 अंश के होते हैं।
  • समद्विबाहु त्रिभुज (Isosceles Triangle): दो भुजाएं बराबर होती हैं और बराबर भुजाओं के सामने के कोण भी बराबर होते हैं।
  • विषमबाहु त्रिभुज (Scalene Triangle): तीनों भुजाएं अलग-अलग लंबाई की होती हैं और तीनों कोण भी अलग-अलग होते हैं।
• कोणों के आधार पर (Based on Angles):
  • न्यूनकोण त्रिभुज (Acute-angled Triangle): तीनों कोण 90 अंश से कम होते हैं।
  • समकोण त्रिभुज (Right-angled Triangle): एक कोण 90 अंश का होता है।
  • अधिककोण त्रिभुज (Obtuse-angled Triangle): एक कोण 90 अंश से अधिक होता है।

त्रिभुज का महत्व (Importance of Triangle):

त्रिभुज ज्यामिति (Geometry) और त्रिकोणमिति (Trigonometry) में एक महत्वपूर्ण ज्यामिति आकार है और इसका महत्व कई क्षेत्रों में है जो निचे निहित है:

1. वास्तुकला और निर्माण (Architecture and Construction): इमारतों, पुलों और अन्य संरचनाओं को डिजाइन और बनाने में त्रिभुज एक महत्वपूर्ण भूमिका निभाते हैं। त्रिभुज अपनी स्थिरता और मजबूती के कारण निर्माण में व्यापक रूप से उपयोग किए जाते हैं। इमारतों के ढांचे, पुलों के ट्रस (truss), छतों के आकार आदि में त्रिभुज का उपयोग होता है।
2. इंजीनियरिंग (Engineering): इंजीनियरिंग के विभिन्न क्षेत्रों, जैसे मैकेनिकल, सिविल और एयरोस्पेस इंजीनियरिंग में त्रिभुजों का व्यापक उपयोग होता है। बलों (forces) के विश्लेषण, संरचनाओं की स्थिरता का अध्ययन, और मशीनों के डिजाइन में त्रिभुजों का प्रयोग किया जाता है।
3. सर्वेक्षण और मानचित्रण (Surveying and Mapping): भूमि की माप और मानचित्र बनाने में त्रिभुजों का उपयोग किया जाता है। त्रिकोणीयकरण (triangulation) विधि का उपयोग करके दूरियों और ऊंचाइयों को सटीक रूप से मापा जा सकता है।
4. नेविगेशन (Navigation): समुद्री और हवाई जहाज के नेविगेशन में त्रिकोणमिति का उपयोग किया जाता है। त्रिभुजों की मदद से दूरी, दिशा और स्थिति की गणना की जाती है।
5. कंप्यूटर ग्राफिक्स (Computer Graphics): 3D मॉडलिंग और एनिमेशन में त्रिभुजों का उपयोग वस्तुओं और दृश्यों को बनाने के लिए किया जाता है। जटिल आकृतियों को छोटे-छोटे त्रिभुजों में विभाजित करके प्रदर्शित किया जाता है।
6. भौतिकी (Physics): प्रकाशिकी (optics), यांत्रिकी (mechanics) और अन्य भौतिकी के क्षेत्रों में त्रिभुजों और त्रिकोणमिति का उपयोग होता है।
7. गणित (Mathematics): त्रिभुज ज्यामिति और त्रिकोणमिति का आधार हैं। त्रिभुजों के गुणों और सूत्रों का अध्ययन गणितीय अवधारणाओं को समझने में मदद करता है।

त्रिभुज गणक का महत्व (Importance of Triangle Calculator):

त्रिभुज गणक एक ऐसा उपकरण है जो त्रिभुज से जुड़ी विभिन्न गणनाओं को बहुत आसान बनाता है। इसका महत्व निम्नलिखित बिंदुओं से समझा जा सकता है:

1. समय की बचत (Time Saving): त्रिभुज के क्षेत्रफल, परिमाप, भुजाओं की लंबाई, और कोणों की गणना मैन्युअल रूप से करने में समय लग सकता है। त्रिभुज गणक इन गणनाओं को तुरंत और सटीक रूप से कर देता है।
2. सटीकता (Accuracy): मैन्युअल गणनाओं में त्रुटि की संभावना अधिक होती है। त्रिभुज गणक सटीक परिणाम प्रदान करता है, जिससे गलतियों की संभावना कम हो जाती है।
3. जटिल समस्याओं का समाधान (Solving Complex Problems): कई बार त्रिभुज से संबंधित समस्याएं जटिल हो सकती हैं, जैसे कि विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करना या अज्ञात भुजा की लंबाई निकालना। त्रिभुज गणक इन समस्याओं को आसानी से हल कर सकता है।
4. शैक्षिक उपकरण (Educational Tool): छात्रों के लिए त्रिभुज गणक एक बेहतरीन शैक्षिक उपकरण है। यह उन्हें त्रिभुज के गुणों और सूत्रों को समझने और अभ्यास करने में मदद करता है।
5. व्यावसायिक उपयोग (Professional Use): इंजीनियरों, वास्तुकारों, सर्वेक्षकों और अन्य पेशेवरों के लिए त्रिभुज गणक एक आवश्यक उपकरण है जो उनके काम को आसान और अधिक कुशल बनाता है।

इस त्रिभुज गणक की विशेषताएं (Features of this Triangle Calculator):

यह त्रिभुज गणक एक बहुमुखी और उपयोगकर्ता के अनुकूल गणक है, जिसमें निम्नलिखित विशेषताएं हैं:

1. बहुभाषी समर्थन (Multilingual Support): यह गणक अंग्रेजी और हिंदी दोनों भाषाओं में उपलब्ध है, जिससे उपयोगकर्ता अपनी पसंदीदा भाषा में इसका उपयोग कर सकते हैं।
2. विभिन्न प्रकार के त्रिभुजों की गणना (Calculation of Different Types of Triangles): यह गणक समबाहु, समद्विबाहु, विषमबाहु और समकोण त्रिभुजों सहित विभिन्न प्रकार के त्रिभुजों के लिए गणनाएँ कर सकता है।
3. विभिन्न पैरामीटर की गणना (Calculation of Different Parameters): यह गणक त्रिभुज के क्षेत्रफल, परिमाप, भुजाओं की लंबाई, ऊँचाई और कोणों की गणना कर सकता है।
4. विभिन्न इकाइयों का समर्थन (Support for Different Units): यह गणक मिलीमीटर (mm), सेंटीमीटर (cm), मीटर (m), किलोमीटर (km), इंच (in) और फीट (ft) जैसी विभिन्न इकाइयों का समर्थन करता है।
5. परिणामों का प्रदर्शन (Display of Results): गणक स्पष्ट और समझने योग्य प्रारूप में परिणाम प्रदर्शित करता है, साथ ही गणना के चरणों को भी दिखाता है।
6. उपयोगकर्ता के अनुकूल इंटरफेस (User-Friendly Interface): गणक का इंटरफेस सरल और उपयोग में आसान है, जिससे किसी भी उपयोगकर्ता, यहां तक कि शुरुआती लोगों के लिए भी इसका उपयोग करना आसान हो जाता है।
7. रिफ्रेश, प्रिंट और शेयर विकल्प (Refresh, Print, and Share Options): उपयोगकर्ता आसानी से इनपुट को रीफ्रेश कर सकते हैं, परिणामों को प्रिंट कर सकते हैं, या उन्हें दूसरों के साथ साझा कर सकते हैं।
8. उदाहरण (Example): इनपुट फ़ील्ड्स के निचे उदहारण भी दिए गए हैं। जो आपको इस कैलकुलेटर को समझने में और आसान बना देता है।

त्रिभुज गणक का उपयोग कैसे करें (How to Use the Triangle Calculator):

इस त्रिभुज गणक का उपयोग करना बहुत ही सरल है। यहां चरण-दर-चरण निर्देश दिए गए हैं:

1. त्रिभुज का प्रकार चुनें: सबसे पहले, उस त्रिभुज के प्रकार का चयन करें जिसकी आप गणना करना चाहते हैं (समबाहु, समद्विबाहु, विषमबाहु, या सामान्य त्रिभुज)। मुख्य बटनों में से एक पर क्लिक करें।
2. गणना का प्रकार चुनें: फिर, उस गणना के प्रकार का चयन करें जिसे आप करना चाहते हैं (जैसे, क्षेत्रफल, परिमाप, भुजा, आदि)। उपलब्ध बटनों में से एक पर क्लिक करें।
3. मान दर्ज करें: आवश्यक मान दर्ज करें, जैसे कि भुजाओं की लंबाई, कोण, या क्षेत्रफल। सुनिश्चित करें कि आप सही इकाई (mm, cm, m, आदि) का चयन करें। इनपुट फ़ील्ड्स के निचे उदहारण भी दिए गए हैं.
4. "गणना करें" बटन पर क्लिक करें: सभी आवश्यक मान दर्ज करने के बाद, "गणना करें" ("Calculate") बटन पर क्लिक करें।
5. परिणाम देखें: गणक तुरंत परिणाम प्रदर्शित करेगा। परिणाम में गणना किए गए मान, उपयोग किए गए सूत्र और गणना के चरण शामिल होंगे।
6. रिफ्रेश, प्रिंट या शेयर करें: आप "रिफ्रेश करें" ("Refresh") बटन पर क्लिक करके इनपुट को साफ कर सकते हैं, "प्रिंट करें" ("Print") बटन पर क्लिक करके परिणामों को प्रिंट कर सकते हैं, या "शेयर करें" ("Share") बटन पर क्लिक करके उन्हें दूसरों के साथ साझा कर सकते हैं।
7. भाषा बदलें (वैकल्पिक): यदि आप भाषा बदलना चाहते हैं, तो "Switch to हिन्दी / English" बटन पर क्लिक करें।

त्रिभुज के उदाहरण (Examples of Triangle Calculations):

यहां विभिन्न प्रकार के त्रिभुजों के कुछ उदाहरण दिए गए हैं, जिनमें इस गणक का उपयोग करके गणनाएँ की गई हैं:

उदाहरण 1: समबाहु त्रिभुज का क्षेत्रफल (Area of an Equilateral Triangle)

मान लीजिए कि एक समबाहु त्रिभुज की भुजा 10 सेमी है। हमें इसका क्षेत्रफल ज्ञात करना है।

• त्रिभुज का प्रकार: समबाहु त्रिभुज
• गणना का प्रकार: क्षेत्रफल
• भुजा: 10 सेमी
• क्षेत्रफल की इकाई: cm

परिणाम:

      क्षेत्रफल गणना:
भुजा: 10 cm
क्षेत्रफल: (√3 / 4) * 10 cm * 10 cm
              = (√3 / 4) * 0.1 m * 0.1 m
              = 0.0043 m²
              = 43.3013 cm²

उदाहरण 2: समद्विबाहु त्रिभुज का परिमाप (Perimeter of an Isosceles Triangle)

मान लीजिए कि एक समद्विबाहु त्रिभुज की बराबर भुजाएँ 7 सेमी हैं और आधार 4 सेमी है। हमें इसका परिमाप ज्ञात करना है।

• त्रिभुज का प्रकार: समद्विबाहु त्रिभुज
• गणना का प्रकार: परिमाप
• बराबर भुजा: 7 सेमी
• आधार: 4 सेमी

परिणाम:

      परिमाप गणना:
बराबर भुजा: 7 cm
आधार: 4 cm
परिमाप: 2 * 7 cm + 4 cm
        = 2 * 0.07 m + 0.04 m
        = 0.18 m
        = 18 cm

उदाहरण 3: विषमबाहु त्रिभुज का क्षेत्रफल (हेरॉन के सूत्र का उपयोग करके) (Area of a Scalene Triangle (Using Heron's Formula))

मान लीजिए कि एक विषमबाहु त्रिभुज की भुजाएँ 3 सेमी, 4 सेमी और 5 सेमी हैं। हमें इसका क्षेत्रफल ज्ञात करना है।

• त्रिभुज का प्रकार: विषमबाहु त्रिभुज
• गणना का प्रकार: क्षेत्रफल
• भुजा 1: 3 सेमी
• भुजा 2: 4 सेमी
• भुजा 3: 5 सेमी
• क्षेत्रफल की इकाई : cm

परिणाम:

      क्षेत्रफल गणना (हेरॉन का सूत्र):
भुजा 1: 3 cm
भुजा 2: 4 cm
भुजा 3: 5 cm
अर्ध-परिमाप (s): (0.03 m + 0.04 m + 0.05 m) / 2 = 0.06 m
क्षेत्रफल: √((0.06 m) * (0.06 m - 0.03 m) * (0.06 m - 0.04 m) * (0.06 m - 0.05 m))
             = 0.0006 m²
             = 6 cm²

उदाहरण 4: त्रिभुज का आधार ज्ञात करना (क्षेत्रफल और ऊंचाई दी गई है) (Finding the Base of a Triangle (Given Area and Height))

मान लीजिए कि एक त्रिभुज का क्षेत्रफल 25 वर्ग सेमी है और ऊंचाई 5 सेमी है। हमें इसका आधार ज्ञात करना है।

• त्रिभुज का प्रकार : त्रिभुज
• गणना का प्रकार : आधार
• क्षेत्रफल : 25 cm
• ऊंचाई : 5cm

परिणाम:

      आधार गणना:
क्षेत्रफल: 25 cm²
ऊंचाई: 5 cm
आधार: (2 * 25 cm²) / 5 cm
        = (2 * 0.0025 m²) / 0.05 m
        = 0.1 m
        = 10 cm

उदाहरण 5: समबाहु त्रिभुज की भुजा ज्ञात करना (क्षेत्रफल से) (Finding the Side of an Equilateral Triangle (from Area))

मान लीजिए कि एक समबाहु त्रिभुज का क्षेत्रफल 43.3 वर्ग सेमी है। हमें इसकी भुजा ज्ञात करनी है।

• त्रिभुज का प्रकार: समबाहु त्रिभुज
• गणना का प्रकार: भुजा (क्षेत्रफल से)
• क्षेत्रफल: 43.3 सेमी

परिणाम:

      भुजा गणना (क्षेत्रफल से):
क्षेत्रफल: 43.3 cm²
भुजा: √(4 * 43.3 cm² / √3)
          = √(4 * 0.0043 m² / √3)
          = 0.1 m
          = 10 cm