समचतुर्भुज (Rhombus) कैलकुलेटर: सब कुछ जो आपको जानना चाहिए

गणित में, समचतुर्भुज (Rhombus) एक महत्वपूर्ण ज्यामितीय आकार है। यह एक ऐसा चतुर्भुज (quadrilateral) होता है जिसकी चारों भुजाएँ (sides) बराबर लंबाई की होती हैं। इसे समझना और इसके गुणों की गणना करना कई क्षेत्रों में उपयोगी होता है, जैसे कि इंजीनियरिंग, वास्तुकला (architecture), और डिज़ाइन। इसलिए हम समचतुर्भुज, इसके महत्व, और एक उपयोगी समचतुर्भुज कैलकुलेटर के बारे में विस्तार से बताएँगे।

समचतुर्भुज एक महत्वपूर्ण ज्यामितीय आकार है, और यह कैलकुलेटर इसकी गणनाओं को सरल और सुलभ बनाता है। चाहे आप एक छात्र हों, शिक्षक हों, या कोई पेशेवर हों जिसे समचतुर्भुज के गुणों की गणना करने की आवश्यकता है, यह उपकरण आपके लिए बहुत उपयोगी होगा। इसकी बहुभाषी समर्थन, इकाई विकल्प, और चरण-दर-चरण समाधान जैसी सुविधाएँ इसे और भी शक्तिशाली बनाती हैं।

समचतुर्भुज (Rhombus) क्या है?

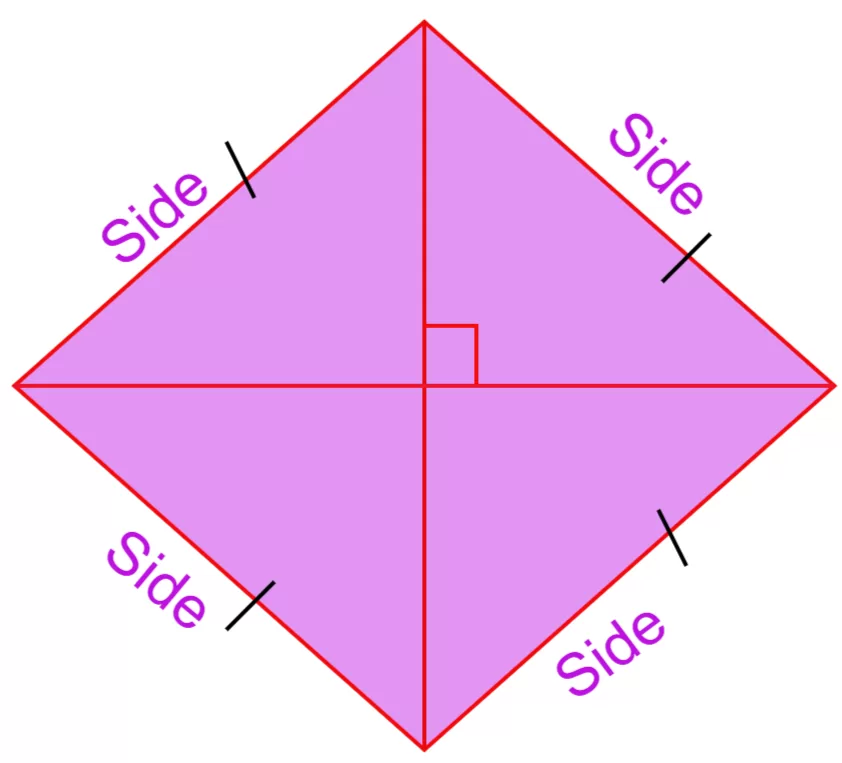
समचतुर्भुज एक विशेष प्रकार का समांतर चतुर्भुज (parallelogram) होता है। समांतर चतुर्भुज में, विपरीत भुजाएँ (opposite sides) समानांतर (parallel) और बराबर होती हैं। समचतुर्भुज में, सभी भुजाएँ बराबर होती हैं। इसके मुख्य गुण (properties) निम्नलिखित हैं:

• चारों भुजाएँ बराबर लंबाई की होती हैं।
• विपरीत कोण (opposite angles) बराबर होते हैं।
• विकर्ण (diagonals) एक दूसरे को समकोण (right angle) पर समद्विभाजित (bisect) करते हैं, यानी 90 डिग्री पर काटते हैं और एक दूसरे को दो बराबर भागों में बाँटते हैं।
• विकर्ण कोणों को भी समद्विभाजित करते हैं।
• समचतुर्भुज का क्षेत्रफल (area) उसके विकर्णों के गुणनफल (product) का आधा होता है।

महत्वपूर्ण अंतर: एक वर्ग (square) भी एक समचतुर्भुज होता है, लेकिन हर समचतुर्भुज एक वर्ग नहीं होता। वर्ग में चारों कोण भी समकोण (90 डिग्री) होते हैं, जबकि समचतुर्भुज में केवल विपरीत कोण बराबर होते हैं (समकोण होना ज़रूरी नहीं है)।

इस समचतुर्भुज कैलकुलेटर का महत्व

समचतुर्भुज के गुणों की गणना करना कभी-कभी जटिल (complex) हो सकता है, खासकर जब आपको विकर्णों, भुजाओं, ऊंचाई, या क्षेत्रफल में से किसी एक को निकालना हो। यह समचतुर्भुज कैलकुलेटर इस प्रक्रिया को बहुत आसान बनाता है। इसके निम्नलिखित लाभ हैं:

• समय की बचत: मैन्युअल रूप से गणना करने के बजाय, आप बस कुछ मान दर्ज करके तुरंत परिणाम प्राप्त कर सकते हैं।
• सटीकता (Accuracy): कैलकुलेटर सटीक गणनाएँ करता है, जिससे मानवीय त्रुटि (human error) की संभावना कम हो जाती है।
• समझने में आसानी: कैलकुलेटर न केवल परिणाम देता है, बल्कि गणना के चरणों को भी दिखाता है, जिससे आप समझ सकते हैं कि परिणाम कैसे प्राप्त हुआ।
• विभिन्न गणनाएँ: यह कैलकुलेटर क्षेत्रफल, परिमाप (perimeter), भुजा, विकर्ण, और ऊंचाई सहित विभिन्न प्रकार की गणनाएँ कर सकता है।
• शैक्षिक उद्देश्य (Educational Purpose): यह छात्रों और शिक्षकों के लिए समचतुर्भुज के गुणों को सीखने और सिखाने का एक बेहतरीन उपकरण है।

इस समचतुर्भुज कैलकुलेटर की विशेषताएँ

यह समचतुर्भुज कैलकुलेटर कई उन्नत सुविधाओं के साथ आता है:

• बहुभाषी समर्थन (Multilingual Support): यह कैलकुलेटर हिंदी और अंग्रेजी दोनों भाषाओं में उपलब्ध है।
• इकाई विकल्प (Unit Options): आप मिलीमीटर (mm), सेंटीमीटर (cm), मीटर (m), किलोमीटर (km), इंच (in), और फीट (ft) जैसी विभिन्न इकाइयों में मान दर्ज कर सकते हैं। कैलकुलेटर स्वचालित रूप से इकाइयों को परिवर्तित (convert) कर देगा।
• चरण-दर-चरण समाधान (Step-by-Step Solution): यह कैलकुलेटर केवल अंतिम उत्तर ही नहीं देता, बल्कि गणना के प्रत्येक चरण को विस्तार से दिखाता है।
• उपयोगकर्ता के अनुकूल इंटरफेस (User-Friendly Interface): इसका इंटरफ़ेस सरल और उपयोग में आसान है।
• विभिन्न गणना विकल्प: आप क्षेत्रफल, परिमाप, भुजा, विकर्ण, और ऊंचाई की गणना कर सकते हैं।
• रिफ्रेश, प्रिंट और शेयर विकल्प: आप आसानी से इनपुट रीसेट कर सकते हैं, परिणामों को प्रिंट कर सकते हैं, और उन्हें दूसरों के साथ साझा कर सकते हैं।

समचतुर्भुज कैलकुलेटर का उपयोग कैसे करें

इस कैलकुलेटर का उपयोग करना बहुत आसान है। यहां विभिन्न गणनाओं के लिए चरण-दर-चरण निर्देश दिए गए हैं:

1. आधार और ऊंचाई का उपयोग करके क्षेत्रफल (Area using Base and Height)
2. सबसे पहले, साइडबार में दिए गए विकल्पों में से “आधार और ऊंचाई द्वारा क्षेत्रफल” चुनें।
3. “आधार” फ़ील्ड में समचतुर्भुज के आधार की लंबाई दर्ज करें।
4. आधार के लिए उचित इकाई (mm, cm, m, km, in, ft) चुनें।
5. “ऊंचाई” फ़ील्ड में समचतुर्भुज की ऊंचाई दर्ज करें।
6. ऊंचाई के लिए उचित इकाई चुनें।
7. परिणामी क्षेत्रफल के लिए उचित इकाई चुनें.
8. “गणना करें” बटन पर क्लिक करें।
9. कैलकुलेटर क्षेत्रफल की गणना करेगा और चरण-दर-चरण समाधान के साथ परिणाम प्रदर्शित करेगा। उदाहरण:
   मान लीजिए कि एक समचतुर्भुज का आधार 10 मीटर है और ऊंचाई 5 मीटर है।
   क्षेत्रफल = आधार × ऊंचाई = 10 m × 5 m = 50 वर्ग मीटर
10. विकर्णों का उपयोग करके क्षेत्रफल (Area using Diagonals)
    1. साइडबार में, “विकर्णों द्वारा क्षेत्रफल” चुनें।
    2. “पहला विकर्ण” फ़ील्ड में पहले विकर्ण की लंबाई दर्ज करें।
    3. पहले विकर्ण के लिए इकाई चुनें।
    4. “दूसरा विकर्ण” फ़ील्ड में दूसरे विकर्ण की लंबाई दर्ज करें।
    5. दूसरे विकर्ण के लिए इकाई चुनें।
    6. परिणामी क्षेत्रफल के लिए उचित इकाई चुनें.
    7. “गणना करें” बटन पर क्लिक करें।
    8. कैलकुलेटर क्षेत्रफल की गणना करेगा और चरण-दर-चरण समाधान दिखाएगा।
    उदाहरण:
    यदि एक समचतुर्भुज के विकर्ण 8 सेमी और 6 सेमी हैं:
    क्षेत्रफल = (1/2) × 8 cm × 6 cm = 24 वर्ग सेमी
11. क्षेत्रफल से ऊंचाई (Height from Area)
    1. “क्षेत्रफल से ऊंचाई” विकल्प चुनें।
    2. “क्षेत्रफल” फ़ील्ड में समचतुर्भुज का क्षेत्रफल दर्ज करें।
    3. क्षेत्रफल के लिए इकाई चुनें।
    4. “आधार” फ़ील्ड में आधार की लंबाई दर्ज करें।
    5. आधार के लिए इकाई चुनें।
    6. परिणामी ऊंचाई के लिए उचित इकाई चुनें.
    7. “गणना करें” बटन पर क्लिक करें।
    8. कैलकुलेटर ऊंचाई की गणना करेगा और चरणों को प्रदर्शित करेगा।
    उदाहरण:
    यदि क्षेत्रफल 20 वर्ग मीटर है और आधार 10 मीटर है:
    ऊंचाई = क्षेत्रफल / आधार = 20 m² / 10 m = 2 मीटर
12. क्षेत्रफल से आधार (Base from Area)
    • “क्षेत्रफल से आधार” विकल्प चुनें।
    • “क्षेत्रफल” फ़ील्ड में क्षेत्रफल दर्ज करें।
    • क्षेत्रफल के लिए इकाई चुनें।
    • “ऊंचाई” फ़ील्ड में ऊंचाई दर्ज करें।
    • ऊंचाई के लिए इकाई चुनें।
    • परिणामी आधार के लिए उचित इकाई चुनें.
    • “गणना करें” बटन पर क्लिक करें।
    • उदाहरण:
      यदि क्षेत्रफल 20 वर्ग मीटर है और ऊंचाई 4 मीटर है:
      आधार = क्षेत्रफल / ऊंचाई = 20 m² / 4 m = 5 मीटर
13. क्षेत्रफल से विकर्ण (Diagonal from Area)
    1. “क्षेत्रफल से विकर्ण” विकल्प चुनें।
    2. “क्षेत्रफल” फ़ील्ड में क्षेत्रफल दर्ज करें।
    3. क्षेत्रफल के लिए इकाई चुनें।
    4. “पहला विकर्ण” फ़ील्ड में पहले विकर्ण की लंबाई दर्ज करें।
    5. पहले विकर्ण के लिए इकाई चुनें।
    6. परिणामी विकर्ण के लिए उचित इकाई चुनें.
    7. “गणना करें” बटन पर क्लिक करें।
    उदाहरण:
    यदि क्षेत्रफल 24 वर्ग सेमी है और पहला विकर्ण 8 सेमी है:
    दूसरा विकर्ण = (2 × क्षेत्रफल) / पहला विकर्ण = (2 × 24 cm²) / 8 cm = 6 सेमी
14. विकर्णों से भुजा (Side from Diagonals)
    1. साइडबार में, “विकर्णों द्वारा भुजा” चुनें।
    2. “पहला विकर्ण” फ़ील्ड में पहले विकर्ण की लंबाई दर्ज करें।
    3. पहले विकर्ण के लिए इकाई चुनें।
    4. “दूसरा विकर्ण” फ़ील्ड में दूसरे विकर्ण की लंबाई दर्ज करें।
    5. दूसरे विकर्ण के लिए इकाई चुनें।
    6. परिणामी भुजा के लिए उचित इकाई चुनें.
    7. “गणना करें” बटन पर क्लिक करें।
    8. कैलकुलेटर भुजा की गणना करेगा और चरण-दर-चरण समाधान दिखाएगा।
    उदाहरण:
    यदि एक समचतुर्भुज के विकर्ण 8 सेमी और 6 सेमी हैं:
    भुजा = √((8² + 6²) / 4) = √(100 / 4) = √25 = 5 cm
15. भुजा से दूसरा विकर्ण (Diagonal from Side)
    1. साइडबार में, “भुजा से विकर्ण” चुनें।
    2. “पहला विकर्ण” फ़ील्ड में पहले विकर्ण की लंबाई दर्ज करें।
    3. पहले विकर्ण के लिए इकाई चुनें।
    4. “भुजा” फ़ील्ड में भुजा की लंबाई दर्ज करें।
    5. दूसरे विकर्ण के लिए इकाई चुनें।
    6. परिणामी विकर्ण के लिए उचित इकाई चुनें.
    7. “गणना करें” बटन पर क्लिक करें।
    8. कैलकुलेटर भुजा की गणना करेगा और चरण-दर-चरण समाधान दिखाएगा।
    उदाहरण:
    यदि एक समचतुर्भुज का पहला विकर्ण 8 cm और भुजा 5 cm हैं:
    दूसरा विकर्ण = √((4 * 5²) – (8²)) = √(100-64) = √36 = 6 cm
16. परिमाप (Perimeter)
    1. “परिमाप” विकल्प चुनें।”भुजा” फ़ील्ड में समचतुर्भुज की एक भुजा की लंबाई दर्ज करें।भुजा के लिए इकाई चुनें।परिणामी परिमाप के लिए उचित इकाई चुनें.”गणना करें” बटन पर क्लिक करें।
    उदाहरण:
    यदि एक समचतुर्भुज की भुजा 5 सेमी है:
    परिमाप = 4 × भुजा = 4 × 5 cm = 20 सेमी