वृत्त कैलकुलेटर : वृत्त से जुड़ी सवालों का हल निकालना अब हुआ आसान।

हम उन्नत वृत्त गणक (Circle Calculator) के बारे में विस्तार से बताएँगे। हम समझेंगे कि वृत्त क्या है, इसका महत्व क्या है, वृत्त गणक की आवश्यकता क्यों होती है, इस विशेष उन्नत गणक की विशेषताएं क्या हैं, और इसका उपयोग कैसे करें। साथ ही, हम वृत्त के 5 उदाहरणों के माध्यम से अवधारणाओं को स्पष्ट करेंगे।

वृत्त क्या है? (What is a Circle?)

वृत्त एक ऐसा ज्यामितीय आकार है जो एक निश्चित बिंदु (केंद्र) से समान दूरी पर स्थित बिंदुओं के समूह से बनता है। इस निश्चित दूरी को त्रिज्या (radius) कहते हैं। वृत्त का आकार पूरी तरह से सममित (symmetrical) होता है। वृत्त के चारों ओर की कुल दूरी को परिधि (circumference) कहते हैं। केंद्र से होकर जाने वाली और वृत्त के दो बिंदुओं को मिलाने वाली रेखा को व्यास (diameter) कहते हैं, जो त्रिज्या का दोगुना होता है।

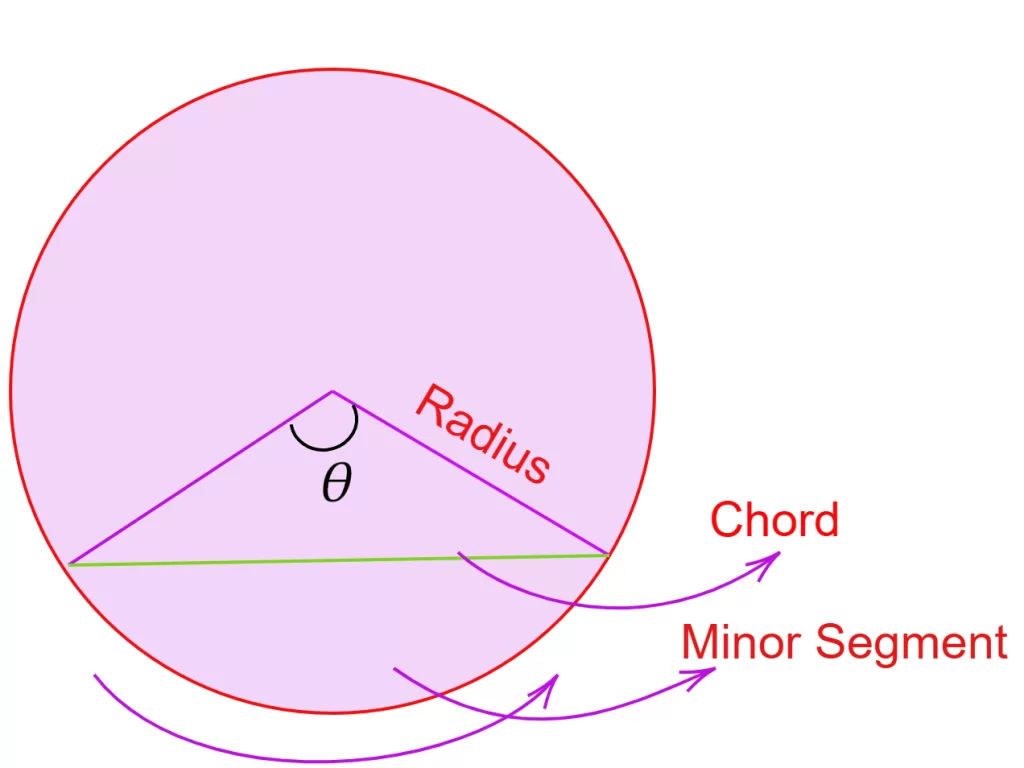
1. वृत्त की त्रिज्या (Radius of Circle):

• परिभाषा: वृत्त के केंद्र (center) से वृत्त की परिधि (circumference) पर स्थित किसी भी बिंदु तक की सीधी दूरी को त्रिज्या कहते हैं। इसे ‘r’ से दर्शाया जाता है। कल्पना कीजिए कि वृत्त एक साइकिल का पहिया है, तो केंद्र से टायर के बाहरी किनारे तक की तीली (spoke) त्रिज्या होगी।
• उदाहरण: यदि एक वृत्त के केंद्र से उसकी परिधि पर किसी बिंदु की दूरी 5 सेंटीमीटर है, तो उस वृत्त की त्रिज्या 5 सेमी है।

2. वृत्त की परिधि (Circumference of Circle):

• परिभाषा: वृत्त के चारों ओर की कुल लंबाई को परिधि कहते हैं। जैसे किसी मैदान के चारों ओर बाड़ लगाना हो, तो बाड़ की कुल लंबाई उस वृत्ताकार मैदान की परिधि होगी। इसे ‘C’ से दर्शाया जाता है.
• सूत्र: C = 2πr (जहाँ π ≈ 3.14159 या 22/7)
• उदाहरण: यदि एक वृत्त की त्रिज्या 7 सेमी है, तो उसकी परिधि = 2 * π * 7 सेमी ≈ 44 सेमी होगी।

3. वृत्त का क्षेत्रफल (Area of Circle):

• परिभाषा: वृत्त के अंदर घिरे हुए स्थान की मात्रा को वृत्त का क्षेत्रफल कहते हैं। जैसे एक गोल रोटी या पिज़्ज़ा का आकार, उसका पूरा समतल भाग उसका क्षेत्रफल होगा। इसे ‘A’ से दर्शाया जाता है.
• सूत्र: A = πr²
• उदाहरण: यदि एक वृत्त की त्रिज्या 3 मीटर है, तो उसका क्षेत्रफल = π * (3 m)² ≈ 28.27 वर्ग मीटर होगा।

4. लघु त्रिज्यखंड का क्षेत्रफल (Area of Minor Sector):

• परिभाषा: वृत्त के केंद्र से दो त्रिज्याओं और उनके बीच के छोटे चाप (arc) से घिरे हुए क्षेत्र को लघु त्रिज्यखंड कहते हैं। यह पिज़्ज़ा के एक छोटे टुकड़े जैसा दिखता है।
• सूत्र: A = (θ/360°) * πr² (जहाँ θ केंद्रीय कोण डिग्री में है) या A = (1/2) * r² * θ (जहाँ θ केंद्रीय कोण रेडियन में है)
• उदाहरण: यदि वृत्त की त्रिज्या 10 सेमी है और केंद्रीय कोण 60° है, तो लघु त्रिज्यखंड का क्षेत्रफल = (60°/360°) * π * (10 cm)² ≈ 52.36 वर्ग सेमी होगा।

5. दीर्घ त्रिज्यखंड का क्षेत्रफल (Area of Major Sector):

• परिभाषा: वृत्त के केंद्र से दो त्रिज्याओं और उनके बीच के बड़े चाप से घिरे हुए क्षेत्र को दीर्घ त्रिज्यखंड कहते हैं। यह पिज़्ज़ा के उस भाग जैसा है जो एक टुकड़ा निकालने के बाद बचता है।
• सूत्र: A = [(360° – θ)/360°] * πr² (θ डिग्री में) या A = (1/2) * r² * (2π – θ) (θ रेडियन में)
• उदाहरण: यदि त्रिज्या 6 सेमी है और केंद्रीय कोण 270° है (जो कि दीर्घ त्रिज्यखंड परिभाषित करता है, क्योंकि यह 180° से बड़ा है), तो दीर्घ त्रिज्यखंड का क्षेत्रफल = [(360°-270°)/360°] * π *(6cm)² = (90°/360°) * π * 36 cm² ≈ 28.27 वर्ग सेमी. यह लघु त्रिज्‍यखंड का क्षेत्रफल निकल गया, क्‍योंकि 270 अंश वास्‍तव में लघु त्रिज्‍यखंड को परिभाषित कर रहा था. सही उदाहरण के लिए, मान लीजिये केन्‍द्रीय कोण 300 अंश है (दीर्घ त्रिज्‍यखंड के लिए). तब, A = [(360°-300°)/360°] * π (6cm)² = (60/360) π * 36 ≈ 18.85 cm² यह गलत है, दीर्घ त्रिज्यखंड का क्षेत्रफल होगा A = (300°/360°) * π * (6 cm)² ≈ 94.25 वर्ग सेमी होगा

6. लघु वृत्तखंड का क्षेत्रफल (Area of Minor Segment):

• परिभाषा: वृत्त की एक जीवा (chord) और उस जीवा द्वारा काटे गए छोटे चाप से घिरे क्षेत्र को लघु वृत्तखंड कहते हैं। यह एक धनुष (bow) और उसकी डोरी (bowstring) के बीच के क्षेत्र जैसा दिखता है।
• सूत्र: A = (1/2) * r² * (θ – sinθ) (θ रेडियन में)
• उदाहरण: यदि त्रिज्या 8 सेमी है और केंद्रीय कोण 90° (π/2 रेडियन) है, तो लघु वृत्तखंड का क्षेत्रफल = (1/2) * (8 cm)² * (π/2 – sin(π/2)) ≈ (1/2) * 64 * (1.57 – 1) ≈ 18.24 वर्ग सेमी।

7. दीर्घ वृत्तखंड का क्षेत्रफल (Area of Major Segment):

• परिभाषा: वृत्त की एक जीवा और उस जीवा द्वारा काटे गए बड़े चाप से घिरे क्षेत्र को दीर्घ वृत्तखंड कहते हैं।
• सूत्र: A = πr² – [(1/2) * r² * (θ – sinθ)] (θ रेडियन में, लघु वृत्तखंड के कोण के लिए). यानी, पूरे वृत्त के क्षेत्रफल में से लघु वृत्तखंड का क्षेत्रफल घटा दें.
• उदाहरण: यदि त्रिज्या 12 cm है और लघु वृत्तखंड का केंद्रीय कोण 60° है, तो पहले लघु वृत्तखंड का क्षेत्रफल निकालें: θ = 60 * (π/180) = π/3 रेडियन. A_minor = (1/2)(12^2)(π/3 – sin(π/3)) = 72 * (1.047 – 0.866) = 72 * 0.181 ≈ 13.03 cm². फिर, वृत्त का क्षेत्रफल: A_circle = π * 12² ≈ 452.39 cm². दीर्घ वृत्तखंड का क्षेत्रफल = 452.39 – 13.03 ≈ 439.36 cm².

8. लघु चाप की लंबाई (Length of Minor Arc):

• परिभाषा: वृत्त की परिधि का वह छोटा हिस्सा जो दो त्रिज्याओं के बीच होता है, लघु चाप कहलाता है।
• सूत्र: L = (θ/360°) * 2πr (θ डिग्री में) या L = rθ (θ रेडियन में)
• उदाहरण: यदि त्रिज्या 9 सेमी है और केंद्रीय कोण 45° है, तो लघु चाप की लंबाई = (45°/360°) * 2 * π * 9 cm ≈ 7.07 सेमी।

9. दीर्घ चाप की लंबाई (Length of Major Arc):

• परिभाषा: वृत्त की परिधि का वह बड़ा हिस्सा जो दो त्रिज्याओं के बीच होता है, दीर्घ चाप कहलाता है।
• सूत्र: L = [(360° – θ)/360°] * 2πr (θ डिग्री में) या L = r(2π – θ) (θ रेडियन में)
• उदाहरण: यदि त्रिज्या 5 मीटर है और केंद्रीय कोण 240° है (जो दीर्घ चाप को परिभाषित करता है), तो दीर्घ चाप की लंबाई = (240°/360°) * 2 * π * 5 m ≈ 20.94 मीटर।

वृत्त का महत्व (Importance of Circle)

वृत्त का हमारे जीवन में और प्रकृति में हर जगह मौजूद हैं:

• पहिए: सबसे महत्वपूर्ण आविष्कारों में से एक, पहिया, वृत्त के आकार का है। गाड़ियों, साइकिलों, और अन्य वाहनों में पहियों का उपयोग होता है।
• प्रकृति: सूर्य, चंद्रमा, और ग्रहों की कक्षाएँ लगभग वृत्ताकार होती हैं। फूलों की पंखुड़ियाँ, पेड़ों के तने, और पानी की बूंदें भी वृत्ताकार या गोलाकार आकार दिखाती हैं।
• इंजीनियरिंग: पुलों, इमारतों, और मशीनों के निर्माण में वृत्ताकार घटकों का व्यापक रूप से उपयोग होता है।
• कला और डिज़ाइन: वृत्त समरूपता और संतुलन का प्रतीक है, और इसका उपयोग कला, वास्तुकला और डिज़ाइन में सुंदरता और सामंजस्य बनाने के लिए किया जाता है।
• गणित: वृत्त ज्यामिति (geometry) और त्रिकोणमिति (trigonometry) का एक मौलिक हिस्सा है।

वृत्त गणक का महत्व (Importance of Circle Calculator)

वृत्त से संबंधित गणनाएँ, जैसे कि क्षेत्रफल (area), परिधि (circumference), त्रिज्या (radius), आदि निकालना, कई बार जटिल हो सकती हैं। वृत्त गणक इन गणनाओं को आसान और तेज़ बनाता है:

• समय की बचत: मैन्युअल रूप से गणना करने में समय लगता है, खासकर जब दशमलव (decimal) संख्याएँ शामिल हों। गणक सेकंडों में परिणाम दे देता है।
• सटीकता: मानवीय त्रुटि की संभावना कम हो जाती है, जिससे सटीक परिणाम मिलते हैं।
• शिक्षा: छात्र वृत्त की अवधारणाओं को बेहतर ढंग से समझने के लिए गणक का उपयोग कर सकते हैं।
• पेशेवर उपयोग: इंजीनियर, आर्किटेक्ट, और डिज़ाइनर अपने काम में वृत्त गणक का उपयोग करते हैं।

इस उन्नत वृत्त गणक की विशेषताएं (Features of this Circle Calculator)

यह वृत्त गणक एक शक्तिशाली और बहुमुखी उपकरण है, जिसमें निम्नलिखित विशेषताएं हैं:

• बहु-कार्यक्षमता: यह वृत्त का क्षेत्रफल, परिधि, त्रिज्या (क्षेत्रफल और परिधि दोनों से), लघु त्रिज्यखंड का क्षेत्रफल, दीर्घ त्रिज्यखंड का क्षेत्रफल, लघु वृत्तखंड का क्षेत्रफल, दीर्घ वृत्तखंड का क्षेत्रफल, लघु चाप की लंबाई, और दीर्घ चाप की लंबाई की गणना कर सकता है।
• इकाई चयन: आप त्रिज्या, क्षेत्रफल, और लंबाई के लिए विभिन्न इकाइयों (मिलीमीटर, सेंटीमीटर, मीटर, किलोमीटर, इंच, फीट, आदि) का चयन कर सकते हैं।
• चरण-दर-चरण समाधान: यह गणक न केवल अंतिम परिणाम देता है, बल्कि गणना के प्रत्येक चरण को भी विस्तार से दिखाता है, जिससे समझना आसान हो जाता है।
• भाषा विकल्प: आप अंग्रेजी और हिंदी के बीच स्विच कर सकते हैं।
• प्रिंट और साझा करें: आप गणना परिणामों को प्रिंट कर सकते हैं या साझा कर सकते हैं।
• स्पष्ट उदाहरण: प्रत्येक गणना के लिए उदाहरण दिए गए हैं ताकि यह समझना आसान हो सके कि जानकारी कैसे दर्ज करें।
• रिफ्रेश बटन: यह बटन आपको सभी इनपुट और परिणामों को तुरंत साफ करने की अनुमति देता है।

वृत्त गणक का उपयोग कैसे करें ? (How to Use the Circle Calculator ?)

इस गणक का उपयोग करना बहुत सरल है। यहां चरण-दर-चरण निर्देश दिए गए हैं:

1. गणना का प्रकार चुनें: सबसे पहले, वह गणना चुनें जो आप करना चाहते हैं (जैसे, “वृत्त का क्षेत्रफल”, “परिधि”, आदि)। मुख्य बटनों पर क्लिक करने से संबंधित इनपुट फ़ील्ड खुल जाएंगे।
2. जानकारी दर्ज करें: आवश्यक जानकारी (जैसे, त्रिज्या, कोण, आदि) इनपुट फ़ील्ड में दर्ज करें। उदाहरण के लिए, वृत्त के क्षेत्रफल की गणना करने के लिए, आपको त्रिज्या दर्ज करनी होगी।
3. इकाइयां चुनें: त्रिज्या, क्षेत्रफल, या लंबाई के लिए उपयुक्त इकाइयां चुनें।
4. “गणना करें” बटन पर क्लिक करें: जानकारी दर्ज करने और इकाइयां चुनने के बाद, “गणना करें” बटन पर क्लिक करें।
5. परिणाम देखें: गणक आपको चरण-दर-चरण समाधान के साथ अंतिम परिणाम दिखाएगा।
6. रिफ्रेश, प्रिंट, या साझा करें: आप “रिफ्रेश” बटन से इनपुट और परिणाम साफ़ कर सकते हैं, “प्रिंट” बटन से परिणाम प्रिंट कर सकते हैं, या “साझा करें” बटन से परिणाम साझा कर सकते हैं।

विशिष्ट गणनाओं के लिए चरण (Steps for Specific Calculations):

• वृत्त का क्षेत्रफल (Area of Circle):
  1. “Area of Circle / वृत्त का क्षेत्रफल” बटन पर क्लिक करें।
  2. “त्रिज्या” फ़ील्ड में त्रिज्या का मान दर्ज करें। उदाहरण: 5
  3. “त्रिज्या की इकाई” चुनें (जैसे, cm)।
  4. “क्षेत्रफल की इकाई” चुनें (जैसे, cm²)।
  5. “गणना करें” बटन पर क्लिक करें।
• परिधि (Circumference):
  1. “Circumference / परिधि” बटन पर क्लिक करें।
  2. त्रिज्या दर्ज करें।
  3. त्रिज्या और परिधि की इकाइयां चुनें।
  4. गणना करें।
• त्रिज्या (क्षेत्रफल से) (Radius from Area):
  1. “Radius (from Area) / त्रिज्या (क्षेत्रफल से)” बटन पर क्लिक करें।
  2. क्षेत्रफल दर्ज करें
  3. क्षेत्रफल और त्रिज्या की इकाइयां चुनें।
  4. गणना करें
• त्रिज्या (परिधि से) (Radius from Circumference):
  1.”Radius (from Circumference) / त्रिज्या (परिधि से)” बटन पर क्लिक करें।
  2.परिधि दर्ज करें
  3.परिधि और त्रिज्या की इकाइयां चुनें।
  4. गणना करें
• लघु त्रिज्यखंड का क्षेत्रफल (Minor Sector Area):
  1. “Minor Sector Area / लघु त्रिज्यखंड का क्षेत्रफल” बटन पर क्लिक करें।
     2.त्रिज्या और कोण (डिग्री में) दर्ज करें।
     3.त्रिज्या और क्षेत्रफल की इकाइयां चुनें।
     4.गणना करें
• दीर्घ त्रिज्यखंड का क्षेत्रफल, लघु वृत्तखंड का क्षेत्रफल, दीर्घ वृत्तखंड का क्षेत्रफल, लघु चाप की लंबाई, और दीर्घ चाप की लंबाई के लिए भी उपरोक्त चरणों का पालन करें, आवश्यक जानकारी और इकाइयां दर्ज करें।

वृत्त के 5 उदाहरण (5 Examples of Circle)

उदाहरण 1: वृत्त का क्षेत्रफल

मान लीजिए कि एक वृत्त की त्रिज्या 7 सेमी है। इसका क्षेत्रफल ज्ञात कीजिए।

• चरण 1: त्रिज्या (r) = 7 cm
• चरण 2: क्षेत्रफल (A) = πr² = π * (7 cm)² ≈ 153.94 cm²

उदाहरण 2: वृत्त की परिधि

एक वृत्त की त्रिज्या 10 मीटर है। इसकी परिधि ज्ञात कीजिए।

• चरण 1: त्रिज्या (r) = 10 m
• चरण 2: परिधि (C) = 2πr = 2 * π * 10 m ≈ 62.83 m

उदाहरण 3: क्षेत्रफल से त्रिज्या

एक वृत्त का क्षेत्रफल 314 cm² है। इसकी त्रिज्या ज्ञात कीजिए।

• चरण 1: क्षेत्रफल (A) = 314 cm²
• चरण 2: त्रिज्या (r) = √(A/π) = √(314 cm² / π) ≈ 10 cm

उदाहरण 4: परिधि से त्रिज्या

एक वृत्त की परिधि 88 cm है। इसकी त्रिज्या ज्ञात कीजिए।

• चरण 1: परिधि (C) = 88 cm
• चरण 2: त्रिज्या (r) = C / (2π) = 88 cm/ (2 * π) ≈14 cm

उदाहरण 5: लघु त्रिज्यखंड का क्षेत्रफल

एक वृत्त की त्रिज्या 14 सेमी है, और एक त्रिज्यखंड का केंद्रीय कोण 60° है। त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए।

• चरण 1: त्रिज्या (r) = 14 cm, कोण (θ) = 60°
• चरण 2: कोण को रेडियन में बदलें: θ (रेडियन में) = 60° * (π / 180°) = π/3 रेडियन
• चरण 3: क्षेत्रफल (A) = (1/2) * r² * θ = (1/2) * (14 cm)² * (π/3) ≈ 102.63 cm²