हमारे आस-पास की दुनिया में बेलन (Cylinder) आकार की बहुत सारी वस्तुएं हर जगह पर मौजूद हैं, चाहे वो सोडा का एक साधारण केन हो या हमारी गाड़ियों को चलाने वाले जटिल इंजन या किसी प्रकार का पाइप हो। जैसे की हम जानते हैं की बेलन के गुणों, जैसे कि आयतन (Volume) और सतह क्षेत्र (Surface Area) को समझना विभिन्न क्षेत्रों में, इंजीनियरिंग से लेकर रोजमर्रा के DIY (Do It Yourself) प्रोजेक्ट्स तक, महत्वपूर्ण है। यहाँ तक की इसकी शुरुवात प्रभावी ढंग से सबसे पहले विद्यालय में सिखाया जाता है।

इसलिए सबसे पहले यह यह गाइड बेलन कैलकुलेटर की दुनिया में गहराई से उतरता है, यह समझाता है कि ये क्या हैं, इनके उपयोग, ये क्यों महत्वपूर्ण हैं, और आप इनका प्रभावी ढंग से उपयोग कैसे कर सकते हैं।

बेलन कैलकुलेटर से आप क्या समझते है?

यह बेलन कैलकुलेटर एक डिजिटल उन्नत कैलकुलेटर है जिसे बेलन के आयतन(Volume), सतह क्षेत्र, या वक्र सतह क्षेत्र (Curved Surface Area) की तुरंत और सटीक गणना करने के लिए डिज़ाइन किया गया है। यह मैनुअल गणना की आवश्यकता को समाप्त करता है, आप इसके मदद से केवल त्रिज्या और ऊंचाई का मान दर्ज करके ही आप हल जेनेरेट कर सकतें है। जिससे समय की बचत होती है और त्रुटियों कम हो जाता है। इन कैलकुलेटरों को आम तौर पर दो प्रमुख मापदंडों की आवश्यकता होती है जिसे हमने निचे दिया हुआ है।

• त्रिज्या (Radius) (r): वृत्ताकार आधार के केंद्र से किनारे तक की दूरी।
• ऊंचाई (Height) (h): दोनों वृत्ताकार आधारों के बीच की लंबवत दूरी।

बेलन से जुड़ी कुछ महत्वपूर्ण परिभाषाएँ और सूत्र सहित जानकारियाँ।

1. बेलन (Cylinder):

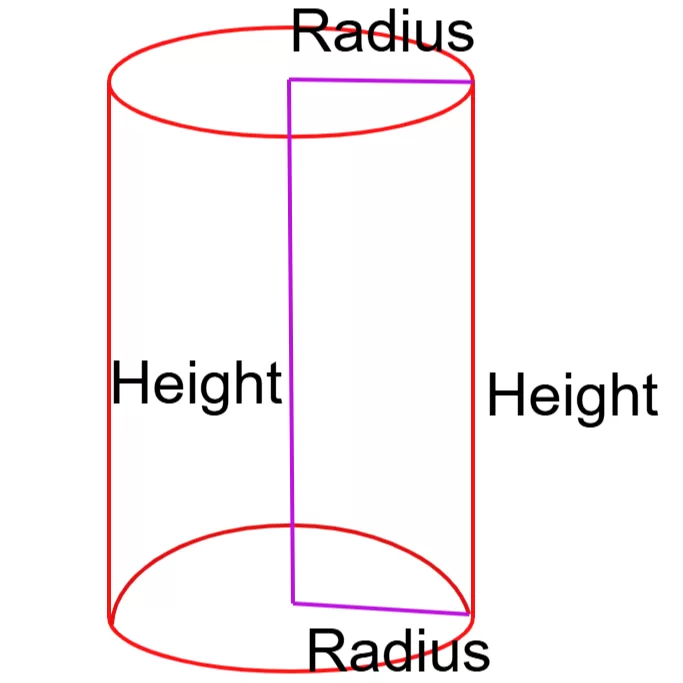
• परिभाषा: बेलन एक ऐसा 3d ठोस आकार होता हैजिसमे दो फेस और वक्र आकर पृष्ठ होता है, आप कल्पना कीजिए जैसे आपने एक वृत्त (circle) को सीधा ऊपर खींचा हो! इसके दो बिल्कुल एक जैसे गोल ढक्कन होते हैं और बीच में एक चिकनी, घुमावदार दीवार। यह डिब्बे जैसा दिखता है, लेकिन गणित की दुनिया में थोड़ा खास है।
• उदाहरण: रसोई में रखे डिब्बे, सड़क बनाने में इस्तेमाल होने वाले रोलर, या यहाँ तक कि पेंसिल वाटर बोतल, कलम भी बेलन के उदाहरण हैं।

2. बेलन की त्रिज्या (Radius):

• परिभाषा: बेलन का गोल सिरा कितना चौड़ा है, यह बताने के लिए हम त्रिज्या का इस्तेमाल करते हैं। यह गोले के केंद्र से उसकी बाहरी किनारे तक की सीधी दूरी है। इसे “r” अक्षर से दिखाते हैं।
• उदाहरण: अगर आपके पास एक बेलन है जिसका गोल सिरा 10 सेंटीमीटर चौड़ा है, तो उसकी त्रिज्या आधी यानी 5 सेंटीमीटर मानी जाती है।

3. बेलन की ऊंचाई (Height):

• परिभाषा: बेलन कितना लंबा है, यह उसकी ऊंचाई से पता चलता है। यह एक गोल ढक्कन से दूसरे गोल ढक्कन तक की सीधी दूरी है। ऊंचाई को “h” अक्षर से दर्शाया जाता है।
• उदाहरण: एक पानी की बोतल बेलन जैसी होती है। अगर बोतल के निचले सिरे से ऊपरी सिरे तक की दूरी 20 सेंटीमीटर है, तो बेलन की ऊंचाई 20 सेंटीमीटर होगी।

4. बेलन का आयतन (Volume):

• परिभाषा: बेलन के अंदर कितनी जगह है, यानी उसमें कितना पानी या कोई और चीज भरी जा सकती है, यह उसका आयतन बताता है।
• सूत्र: बेलन का आयतन निकालने के लिए हम πr²h का इस्तेमाल करते हैं। यहाँ π (पाई) एक खास नंबर है (लगभग 3.14), ‘r’ त्रिज्या है, और ‘h’ ऊंचाई है।
• उदाहरण: अगर एक बेलन की त्रिज्या 4 सेंटीमीटर और ऊंचाई 10 सेंटीमीटर है, तो उसका आयतन लगभग 502.65 घन सेंटीमीटर होगा। इसका मतलब है कि उसमें लगभग 502.65 मिलीलीटर पानी भरा जा सकता है।

5. बेलन का पृष्ठीय क्षेत्रफल (Surface Area):

• परिभाषा: बेलन को बनाने में कुल कितनी सामग्री लगी है, यह जानने के लिए हम पृष्ठीय क्षेत्रफल निकालते हैं। इसमें दोनों गोल ढक्कनों का क्षेत्रफल और बेलन की घुमावदार दीवार का क्षेत्रफल शामिल होता है।
• सूत्र: पृष्ठीय क्षेत्रफल निकालने का सूत्र है: 2πr² + 2πrh
• उदाहरण: एक डिब्बे को बनाने में कितना कागज लगेगा, यह जानने के लिए हम उसके पृष्ठीय क्षेत्रफल की गणना कर सकते हैं।

6. बेलन का वक्र पृष्ठीय क्षेत्रफल (Curved Surface Area):

• परिभाषा: बेलन के गोल ढक्कनों को छोड़कर, सिर्फ घुमावदार दीवार का क्षेत्रफल वक्र पृष्ठीय क्षेत्रफल कहलाता है।
• सूत्र: वक्र पृष्ठीय क्षेत्रफल निकालने का सूत्र है: 2πrh
• उदाहरण: अगर आप किसी बेलनाकार पाइप को रंगना चाहते हैं, तो आपको उसके वक्र पृष्ठीय क्षेत्रफल के हिसाब से रंग की मात्रा का अनुमान लगाना होगा।

बेलन कैलकुलेटर का उपयोग क्या है?

बेलन कैलकुलेटर का प्राथमिक उपयोग बेलन के निम्नलिखित गुणों को निर्धारित करना है:

• आयतन (Volume) (V): बेलन के भीतर समाहित जगह की मात्रा, जिसे घन इकाइयों (Cubic Units) में मापा जाता है (जैसे, घन सेंटीमीटर, घन मीटर, घन इंच)। आयतन का सूत्र है: V = πr²h
• सतह क्षेत्र (Surface Area) (SA): बेलन की बाहरी सतह का कुल क्षेत्रफल, जिसमें दोनों वृत्ताकार आधार और वक्र पक्ष शामिल हैं, जिसे वर्ग इकाइयों (Square Units) में मापा जाता है (जैसे, वर्ग सेंटीमीटर, वर्ग मीटर, वर्ग इंच)। सतह क्षेत्र का सूत्र है: TSA = 2πr² + 2πrh
• वक्र सतह क्षेत्र (Curved Surface Area) (CSA): बेलन के वक्र पक्ष का क्षेत्रफल, जिसमें वृत्ताकार आधार शामिल नहीं हैं, इसे भी वर्ग इकाइयों में मापा जाता है। वक्र सतह क्षेत्र का सूत्र है: CSA = 2πrh

बेलन कैलकुलेटर का महत्व

बेलन कैलकुलेटर कई महत्वपूर्ण लाभ प्रदान करते हैं:

• सटीकता (Accuracy): वे सटीक परिणाम प्रदान करते हैं, मैनुअल गणना में मानवीय त्रुटि की संभावना को समाप्त करते हैं।
• गति (Speed): गणना तुरंत की जाती है, जिससे मूल्यवान समय की बचत होती है, खासकर जब कई बेलनों या जटिल परियोजनाओं से निपटना हो।
• सुविधा (Convenience): ऑनलाइन या मोबाइल ऐप्स के रूप में उपलब्ध, इनका उपयोग कभी भी, कहीं भी किया जा सकता है।
• बहुमुखी प्रतिभा (Versatility): वे विभिन्न क्षेत्रों में उपयोगी हैं, जिनमें शामिल हैं:
  • इंजीनियरिंग (Engineering): टैंक, पाइप और अन्य बेलनाकार संरचनाओं का डिजाइन।
  • निर्माण (Construction): बेलनाकार घटकों के लिए सामग्री की आवश्यकताओं का अनुमान।
  • विनिर्माण (Manufacturing): बेलनाकार कंटेनरों के आयतन की गणना।
  • गणित और शिक्षा (Mathematics and Education): ज्यामितीय अवधारणाओं का प्रदर्शन और सुदृढ़ीकरण।
  • DIY और गृह सुधार (DIY and Home Improvement): प्लांटर्स, पानी के टैंक और अन्य बेलनाकार वस्तुओं की क्षमता की गणना।

इस बेलन कैलकुलेटर का उपयोग कैसे करें?

अधिकांश ऑनलाइन बेलन कैलकुलेटर सहज और उपयोग में आसान होते हैं। यहां एक सामान्य चरण-दर-चरण मार्गदर्शिका दी गई है:

1. आवश्यक मान दर्ज करें (Enter the Required Values): बेलन की त्रिज्या (r) और ऊंचाई (h) को निर्दिष्ट फ़ील्ड में इनपुट करें। सुनिश्चित करें कि आप माप की लगातार इकाइयों का उपयोग करते हैं (जैसे, दोनों सेंटीमीटर में या दोनों इंच में)।
2. वांछित गणना का चयन करें (Select the Desired Calculation): चुनें कि आप आयतन, सतह क्षेत्र, या वक्र सतह क्षेत्र की गणना करना चाहते हैं।
3. परिणाम देखें (View the Results): कैलकुलेटर स्वचालित रूप से गणना किए गए मान को प्रदर्शित करेगा।

वास्तविक जीवन में इस बेलन कैलकुलेटर के कुछ उपयोग इसप्रकार है।

• भंडारण टैंकों का डिजाइन (Designing Storage Tanks): इंजीनियर तरल पदार्थ या गैसों के लिए भंडारण टैंकों के आयतन को निर्धारित करने के लिए बेलन कैलकुलेटर का उपयोग करते हैं।
• पाइप क्षमता का अनुमान (Estimating Pipe Capacity): प्लंबर और निर्माण श्रमिक बेलनाकार पाइपों के माध्यम से बहने वाले पानी या अन्य तरल पदार्थों के आयतन की गणना करने के लिए इनका उपयोग करते हैं।
• पेंट कवरेज की गणना (Calculating Paint Coverage): DIYers बेलनाकार स्तंभों या प्लांटर्स के सतह क्षेत्र को निर्धारित करने और आवश्यक पेंट की मात्रा का अनुमान लगाने के लिए बेलन कैलकुलेटर का उपयोग कर सकते हैं।
• पैकेजिंग आयतन का निर्धारण (Determining Packaging Volume): जैसे की निर्माता भोजन, पेय पदार्थ, या अन्य उत्पादों के लिए बेलनाकार कंटेनरों के आयतन की गणना करने के लिए इनका उपयोग करते हैं।
• आवश्यक कंक्रीट की मात्रा की गणना (Calculating the Amount of Concrete Needed): बिल्डर और ठेकेदार गोलाकार खंभों के लिए आवश्यक कंक्रीट की मात्रा निर्धारित करने के लिए बेलन कैलकुलेटर का उपयोग करते हैं।

बेलन आयतन, सतह क्षेत्र और वक्र सतह क्षेत्र पर आधारित 5 उदाहरण

यहां 5 उदाहरण दिए गए हैं जो बेलन गणना के व्यावहारिक अनुप्रयोग को दर्शाते हैं:

उदाहरण 1: आयतन गणना

• समस्या: एक बेलनाकार पानी की टंकी की त्रिज्या 2 मीटर और ऊंचाई 5 मीटर है। टैंक में कितना पानी आ सकता है?
• समाधान:
  • त्रिज्या (r) = 2 मीटर
  • ऊंचाई (h) = 5 मीटर
  • आयतन (V) = πr²h = π * (2²)* 5 = π * 4 * 5 = 20π ≈ 62.83 घन मीटर

उदाहरण 2: सतह क्षेत्र गणना

• समस्या: एक बेलनाकार धातु के केन की त्रिज्या 3 सेमी और ऊंचाई 8 सेमी है। केन का कुल सतह क्षेत्र क्या है?
• समाधान:
  • त्रिज्या (r) = 3 सेमी
  • ऊंचाई (h) = 8 सेमी
  • सतह क्षेत्र (SA) = 2πr² + 2πrh = 2 * π * (3²) + 2 * π * 3 * 8 = 18π + 48π = 66π ≈ 207.35 वर्ग सेमी

उदाहरण 3: वक्र सतह क्षेत्र गणना

• समस्या: एक बेलनाकार खंभे की त्रिज्या 0.5 मीटर और ऊंचाई 3 मीटर है। खंभे का वक्र सतह क्षेत्र क्या है?
• समाधान:
  • त्रिज्या (r) = 0.5 मीटर
  • ऊंचाई (h) = 3 मीटर
  • वक्र सतह क्षेत्र (CSA) = 2πrh = 2 * π * 0.5 * 3 = 3π ≈ 9.42 वर्ग मीटर

उदाहरण 4: आयतन दिए जाने पर ऊंचाई ज्ञात करना

• समस्या: एक बेलनाकार कंटेनर में 1000 घन सेंटीमीटर तरल पदार्थ भरना है। यदि कंटेनर की त्रिज्या 5 सेमी है, तो ऊंचाई क्या होनी चाहिए?
• समाधान:
  • आयतन (V) = 1000 घन सेमी
  • त्रिज्या (r) = 5 सेमी
  • V = πr²h => h = V / (πr²) = 1000 / (π * 5²) = 1000 / (25π) ≈ 12.73 सेमी

उदाहरण 5: दो बेलनों के आयतन की तुलना करना

• समस्या: बेलन A की त्रिज्या 4 सेमी और ऊंचाई 6 सेमी है। बेलन B की त्रिज्या 6 सेमी और ऊंचाई 4 सेमी है। किस बेलन का आयतन अधिक है?
• समाधान:
  • बेलन A: V = πr²h = π * (4²)* 6 = 96π
• • बेलन B: V = πr²h = π * (6²)* 4 = 144π
  बेलन B का आयतन (144π) बेलन A (96π) से अधिक है।