गोला (Sphere) एक मौलिक ज्यामितीय आकार है जैसे की जो हमारे आसपास मौजूद है, चाहे वो ग्रह हों, गेंदें हों या गोले जैसे वास्तुकला में सजावटी तत्व। गोले के गुणों, जैसे कि आयतन (Volume) और पृष्ठ क्षेत्रफल (Surface Area) को समझना विज्ञान, इंजीनियरिंग, और रोजमर्रा की जिंदगी में महत्वपूर्ण है। यह कालूलेटर मुख्य रूप से विद्यार्थी के लिए ही है। यह जानकारी आपको गोला से जुड़े आयतन या पृष्ठ क्षेत्रफल को कैलकुलेटर की दुनिया में गहराई से उतरता है और आप हमारे द्वारा दिए हुए गोले कैलकुलेटर जो आपके गणित के कैलकुलेशन को सरल बनाने में सक्षम है।

इस कैलकुलेटर द्वारा जेनेरेट किये हुए हल प्रिंट और अपने दोस्तों के पास शेयर भी कर सकते है किये जैसे की इस कैलकुलेटर का उपयोग, कैलकुलेटर क्यों इतना महत्वपूर्ण हैं, और आप इनका प्रभावी ढंग से उपयोग कैसे कर सकते हैं।

गोला कैलकुलेटर से आप क्या समझते है?

गोला कैलकुलेटर एक डिजिटल उपकरण है जिसे गोले के आयतन और पृष्ठ क्षेत्रफल की तुरंत और सटीक गणना करने के लिए किया जाता है। यह मैनुअल गणना की आवश्यकता को समाप्त करता है, जिससे समय की बचत होती है और त्रुटियों का बहुत कम कर देता है। इस कैलकुलेटरों को आम तौर पर एक प्रमुख पैरामीटर की आवश्यकता होती है जिसे समझना जरूरी है:

• त्रिज्या (Radius) (r): गोले के केंद्र से सतह तक की दूरी।

गोले से जुड़े परिभाषा और कुछ महत्व पूर्ण जानकारियाँ।

1. गोला (Sphere): एक गोल मटोल दुनिया जो पृथ्वी को लेकर कल्पना करते है ।

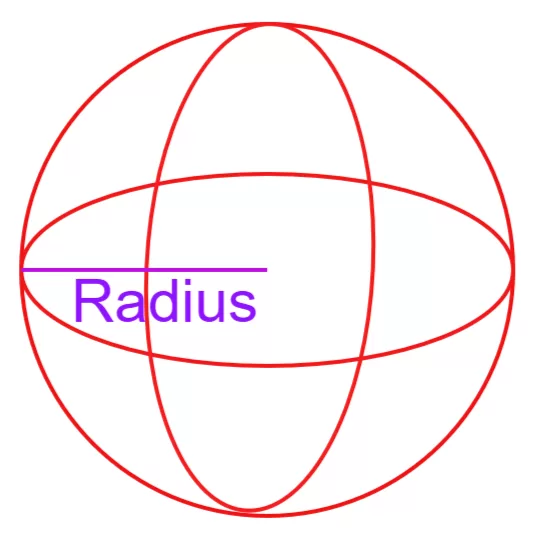
• परिभाषा: गोला एक त्रिविमीय (3D) ज्यामितीय आकृति है। इसे ऐसे समझो जैसे कोई गेंद, जो हर तरफ से गोल हो। गोले के हर बिंदु की दूरी उसके केंद्र से बराबर या सामान होती है।
• आसान भाषा में: यह एक 3D वृत्त है, जिसमें कोई किनारा या कोना नहीं होता।
• उदाहरण: क्रिकेट बॉल, फुटबॉल, बास्केटबॉल, ग्लोब, लड्डू (जो गोल हो!), ये सब गोले के उदाहरण हैं।
• हमारे अंदाज से: गोला एक “परफेक्ट” आकृति है, जिसमें हर दिशा में संतुलन होता है।

2. गोले की त्रिज्या (Radius of Sphere): केंद्र से सतह तक की दूरी होती है ।

• परिभाषा: गोले की त्रिज्या (r) उसके केंद्र से उसकी सतह या पृष्ठ पर स्थित किसी भी बिंदु तक की दूरी होती है।
• आसान भाषा में: अगर आप गोले के बिल्कुल बीच में एक पिन चुभाएं और सतह तक रेखा खींचें, तो उस रेखा की लंबाई ही त्रिज्या है।
• उदाहरण: अगर एक गेंद की त्रिज्या 5 सेंटीमीटर है, तो इसका मतलब है कि गेंद के केंद्र से उसकी बाहरी सतह तक की दूरी 5 सेंटीमीटर है।
• हमारे अंदाज से: त्रिज्या, गोले के आकार की “चाबी” है।

3. गोले का आयतन (Volume of Sphere): अंदर कितना द्रव भर सकता है।

• परिभाषा: गोले का आयतन (V) यह बताता है कि गोले के अंदर कितनी जगह है, यानी उसमें कितनी सामग्री भरी जा सकती है।
• सूत्र: V = (4/3)πr³ (जहां π ≈ 3.14 और r त्रिज्या है)
• आसान भाषा में: सोचो आपके पास एक गुब्बारा है। उसमें जितनी हवा भरी जा सकती है, वह हवा का माप ही गुब्बारे का आयतन है।
• उदाहरण: एक फुटबॉल जिसकी त्रिज्या 10 सेंटीमीटर है, उसका आयतन लगभग 4188.79 घन सेंटीमीटर होगा।
• हमारे अंदाज से: आयतन, किसी गोले की “क्षमता” दिखाता है।

4. गोले का कुल पृष्ठीय क्षेत्रफल (Total Surface Area of Sphere): बाहर के सतह का पूरा माप।

• परिभाषा: गोले का पृष्ठीय क्षेत्रफल (A) उसके बाहरी सतह का कुल क्षेत्रफल होता है।
• सूत्र: A = 4πr² (जहां π = 22/7 या π ≈ 3.14 और r त्रिज्या है)
• आसान भाषा में: अगर आप एक गेंद को कागज या कपड़े से पूरी तरह ढकना चाहें, तो जितना कागज लगेगा, वह कागज या कपड़े का माप ही गेंद का पृष्ठीय क्षेत्रफल है।
• उदाहरण: एक गेंद जिसकी त्रिज्या 7 सेंटीमीटर है, उसका पृष्ठीय क्षेत्रफल लगभग 615.75 वर्ग सेंटीमीटर होगा।
• हमारे अंदाज से: पृष्ठीय क्षेत्रफल, गोले का “कवर” है।

कुछ अतिरिक्त बातें:

• π (पाई) एक गणितीय स्थिरांक है जिसका मान 22/7 होता है। यह गोले के आयतन और पृष्ठीय क्षेत्रफल के सूत्रों में महत्वपूर्ण होता है।
• गोले का केंद्र (center) वह बिंदु है जो गोले के सतह या पृष्ठ से सभी बिंदुओं से समान दूरी पर होता है।
• गोले का व्यास (diameter) त्रिज्या का दोगुना (d = 2r)होता है और यह गोले के केंद्र से होकर गुजरने वाली सबसे लंबी रेखा होती है।

गोला कैलकुलेटर का उपयोग क्या-क्या होता है?

गोला कैलकुलेटर का प्राथमिक उपयोग गोले के निम्नलिखित गुणों को निर्धारित करना है:

• आयतन (Volume) (V): गोले के भीतर समाहित जगह की मात्रा, जिसे घन इकाइयों (Cubic Units) में मापा जाता है (जैसे, घन सेंटीमीटर, घन मीटर, घन इंच)। आयतन का सूत्र है: V = (4/3)πr³
• सतह क्षेत्र (Surface Area) (SA): गोले की बाहरी सतह का कुल क्षेत्रफल, जिसे वर्ग इकाइयों (Square Units) में मापा जाता है (जैसे, वर्ग सेंटीमीटर, वर्ग मीटर, वर्ग इंच)। सतह क्षेत्र का सूत्र है: SA = 4πr²

गोला कैलकुलेटर का महत्व

गोला कैलकुलेटर कई महत्वपूर्ण लाभ प्रदान करता है।

• सटीकता (Accuracy): वे सटीक परिणाम प्रदान करते हैं, मैनुअल गणना में मानवीय त्रुटि की संभावना को समाप्त करते हैं।
• गति (Speed): गणना तुरंत हो ही जाती है, जिससे मूल्यवान समय की बचत होती है, खासकर जब कई गोलों या जटिल परियोजनाओं से निपटना हो।
• सुविधा (Convenience): ऑनलाइन या मोबाइल ऐप्स के रूप में उपलब्ध, इनका उपयोग कभी भी, कहीं भी किया जा सकता है।
• बहुमुखी प्रतिभा (Versatility): वे विभिन्न क्षेत्रों में गोले से जुड़े उपयोगी हैं, जिनमें कुछ शामिल क्षेत्र हैं:
  • खगोल विज्ञान (Astronomy): ग्रहों और अन्य खगोलीय पिंडों के आयतन और सतह क्षेत्र की गणना करने में।
  • इंजीनियरिंग (Engineering): गोलाकार टैंकों, गुंबदों और अन्य गोलाकार संरचनाओं का डिजाइन करने में।
  • रसायन विज्ञान (Chemistry): परमाणुओं और अणुओं के आकार और आयतन का अनुमान करने में।
  • गणित और शिक्षा (Mathematics and Education): ज्यामितीय अवधारणाओं का प्रदर्शन और सुदृढ़ीकरण करने में।
  • DIY और शिल्प (DIY and Craft): गोलाकार वस्तुओं के लिए सामग्री की आवश्यकताओं की गणना करने में।

इस गोला कैलकुलेटर का उपयोग कैसे करें?

अधिकांश ऑनलाइन गोला कैलकुलेटर सहज और उपयोग में आसान होते हैं। यहां भी एक सामान्य चरण-दर-चरण मार्गदर्शिका दी गई है:

1. त्रिज्या दर्ज करें (Enter the Radius): गोले की त्रिज्या (r) को निर्दिष्ट फ़ील्ड में इनपुट करें। सुनिश्चित करें कि आप माप की उपयुक्त इकाई का उपयोग करते हैं (जैसे, सेंटीमीटर, मीटर, इंच)।
2. परिणाम देखें (View the Results): कैलकुलेटर स्वचालित रूप से आयतन और सतह क्षेत्र के गणना किए गए मानों को प्रदर्शित करेगा।
3. यदि आप चाहतें तो आप जेनेरेट किये हुए हल को प्रिंट या शेयर भी करा सकते है।

वास्तविक जीवन में गोला कैलकुलेटर के कुछ उपयोग।

• ग्रहों और तारों के आकार का अनुमान (Estimating the Size of Planets and Stars): खगोलविद ग्रहों और तारों के आयतन और सतह क्षेत्र की गणना करने के लिए गोला के इस कैलकुलेटर का उपयोग करते हैं।
• गोलाकार टैंकों का डिजाइन (Designing Spherical Tanks): इंजीनियर गोलाकार टैंकों के आयतन की गणना करने के लिए गोला कैलकुलेटर का उपयोग करते हैं ताकि वे एक निश्चित मात्रा में तरल पदार्थ या गैस जमा कर सकें।
• गुंबदों और गोलाकार संरचनाओं का निर्माण (Constructing Domes and Spherical Structures): आर्किटेक्ट गुंबदों और अन्य गोलाकार संरचनाओं के लिए आवश्यक सामग्री की मात्रा का अनुमान लगाने के लिए गोला कैलकुलेटर का उपयोग करते हैं।
• रसायन विज्ञान में परमाणुओं और अणुओं का अध्ययन (Studying Atoms and Molecules in Chemistry): रसायनज्ञ परमाणुओं और अणुओं के आयतन और सतह क्षेत्र का अनुमान लगाने के लिए गोला कैलकुलेटर का उपयोग करते हैं ताकि उनके व्यवहार और प्रतिक्रियाशीलता को समझ सकें।
• खेलों में गेंदों का निर्माण (Manufacturing Balls for Sports): गेंद निर्माताओं को यह सुनिश्चित करने के लिए गोले के गुणों को जानना होगा कि वे उचित आकार और वजन के हैं।

गोला आयतन और पृष्ट क्षेत्रफल पर आधारित 5 उदाहरण

यहां 5 उदाहरण दिए गए हैं जो गोला गणना के व्यावहारिक अनुप्रयोग को दर्शाते हैं:

उदाहरण 1: आयतन गणना (Volume Calculation)

• समस्या: एक गेंद की त्रिज्या 5 सेमी है। गेंद का आयतन क्या है?
• समाधान:
  • त्रिज्या (r) = 5 सेमी
  • आयतन (V) = (4/3)πr³ = (4/3) * π * (5³) = (4/3) * π * 125 ≈ 523.60 घन सेमी

उदाहरण 2: सतह क्षेत्र गणना (Surface Area Calculation)

• समस्या: एक गोलाकार गुब्बारे की त्रिज्या 10 सेमी है। गुब्बारे का सतह क्षेत्र क्या है?
• समाधान:
  • त्रिज्या (r) = 10 सेमी
  • सतह क्षेत्र (SA) = 4πr² = 4 * π * (10²) = 4 * π * 100 ≈ 1256.64 वर्ग सेमी

उदाहरण 3: त्रिज्या दिए जाने पर आयतन ज्ञात करना (Finding Volume Given Radius)

• समस्या: एक गोलाकार बर्तन में कितनी जगह होगी यदि उसकी त्रिज्या 8 इंच है?
• समाधान:
  • त्रिज्या (r) = 8 इंच
  • आयतन (V) = (4/3)πr³ = (4/3) * π * (8³) = (4/3) * π * 512 ≈ 2144.66 घन इंच

उदाहरण 4: आयतन दिए जाने पर त्रिज्या ज्ञात करना (Finding Radius Given Volume)

• समस्या: एक गोलाकार पत्थर का आयतन 113.09 घन सेंटीमीटर है। पत्थर की त्रिज्या कितनी है?
• समाधान:
  • आयतन (V) = 113.09 घन सेंटीमीटर
  • V = (4/3)πr³ => r = ∛(3V / 4π) = ∛(3 * 113.09 / (4 * π)) ≈ 3 सेमी

उदाहरण 5: दो गोलों के सतह क्षेत्र की तुलना करना (Comparing Surface Areas of Two Spheres)

• समस्या: गोला A की त्रिज्या 3 सेमी है और गोला B की त्रिज्या 6 सेमी है। किस गोले का सतह क्षेत्र अधिक है और कितना अधिक?
• समाधान:
  • गोला A: SA = 4πr² = 4 * π * (3²) = 36πगोला B: SA = 4πr² = 4 * π * (6²) = 144π
  गोला B का सतह क्षेत्र (144π) गोला A (36π) से अधिक है। यह 144π – 36π = 108π ≈ 339.29 वर्ग सेमी अधिक है।